Designing A Mathematical Bridge To The Metaverse
A proposed theory for linking 2D Websites to 3D Webspheres, with the goal of accelerating user adoption of 3D/virtual/augmented/mixed reality experiences from VR social networks to virtual e-commerce to immersive live-streaming.
My intention here is to lay out a possible framework that can be used by the 3D, VR, AR, MR community to start to define how users interfaces in our current 2D web will work together with those in 3D based virtual environments. There are 25 total pages that I sketched out on my Moleskin over August and September. This post is intended to be a first draft. I have added textual context and explanations to the drawings in page 1–10. I intend to do the same for 11–25, but didn’t want to wait for that to be done to share. After all the perfect is the enemy of the good.
As this is not a piece of software or code, it does not have a license attached to it. That being said, it is my original thinking and I expect that it will be attributed accordingly. My hope is that these thoughts will light fires in the minds of mixed reality designers, users, inventors, and thinkers and play a small part in moving the mixed reality movement forward._
I truly believe that without a “guide” for interpreting 3D environments in our existing 2D web, the pace of adoption of VR/AR technologies will be unnecessarily delayed.
Most importantly, I hope that those of you who have the courage and coffee to read this add your improvements, corrections, and suggested modifications. That way, this can be a living document, perhaps even a theory of some sort, with contributions from as many people as possible.
Page 1: Fluid movement between 2D and 3D
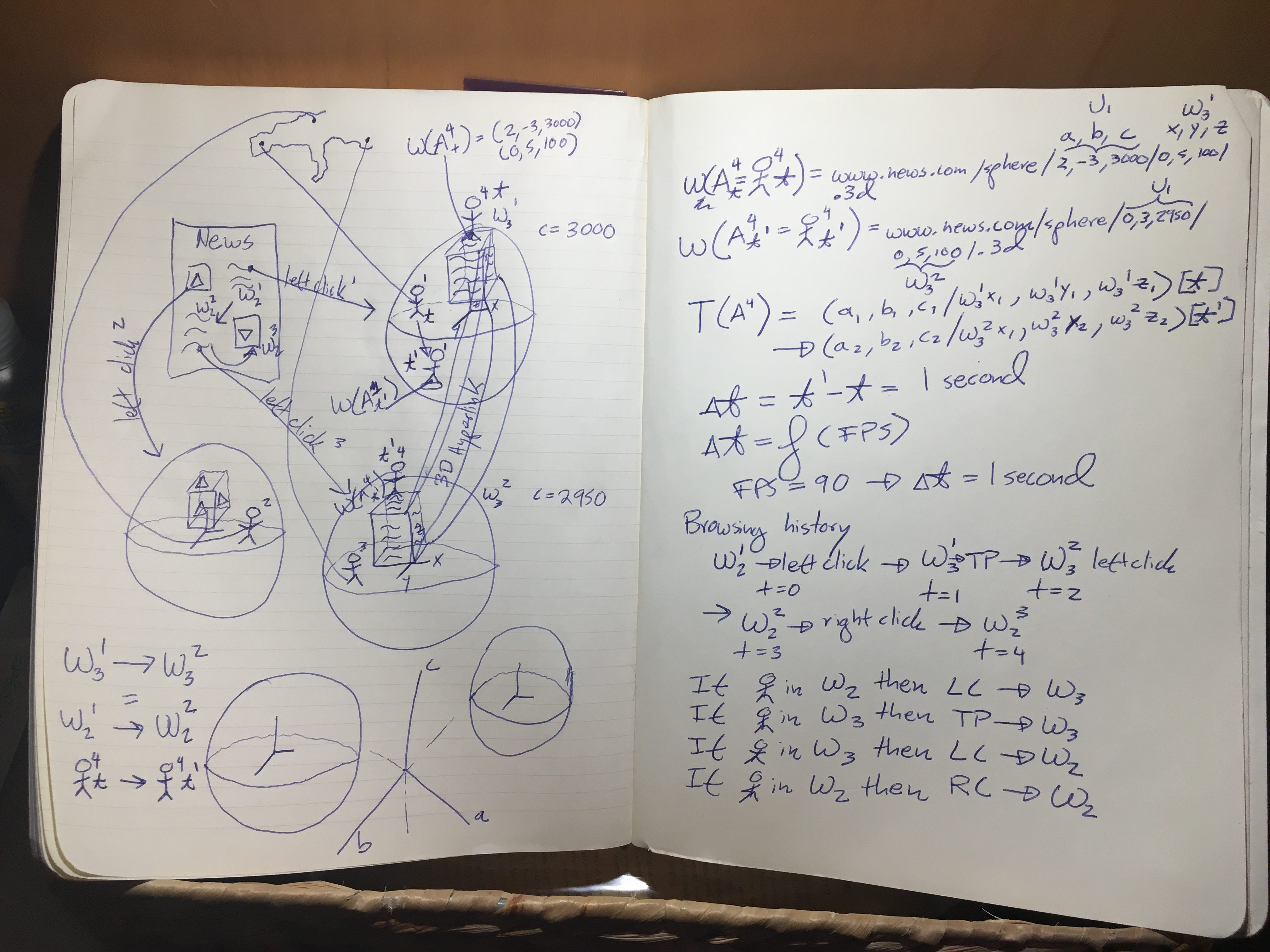
The user starts in 2D reading the article in the upper right hand corner. She left clicks on the article, which transports her to a websphere W(3,1) — which means 3D websphere number 1. The position of the user in 3D is such that she can read the article comfortably. The text of the article could be on a cube, with the portion she is reading facing her initially, and the cube rotating to reveal the whole article.
The avatar shown in W(3,1) corresponds to a user in Madrid, Spain. She can experience the 3D news cube via virtual reality, augmented reality, or merely as a 3D scene on the web. In other words, the user of a headset is not required. That being said, the example here, and in the next pages, assumes that the user is using a headset. The reason this assumption is important is that the field of view emanates directly from the avatar’s eyes, as opposed to a camera placed behind or next to the avatar.
There is an equivalent to this perspective in a non-immersive 3D environment — essentially an “in avatar” viewpoint — something that is commonly used by experienced users of Second Life.
This avatar moves along the (x,y,z) local coordinates from time t to t1. The movement in this case is towards the edge of the sphere. Another avatar A4 is represented as standing above the news cube at time t. The 6 dimensional coordinates of A4 at t denoted as W(A4t) are (2,-3,3000) in the (a,b,c) universal coordinate space and (0,5,100) in the local space.
At time t1 A4 finds himself in a different websphere W(3,2) — meaning 3D websphere number 2.
This new position is the result of A4 having accessed a 3D hyperlink that connects W(3,1) to W(3,2).
W(3,2) is represented as relatively near W(3,1) in the universal coordinate space, thus c = 2950 for A4 in W(3,2) at time t1, whereas c = 3000 for A4 in W(3,1) at time t.
Now here is the tricky part. The news cube in W(3,2) does not contain the same story as W(3,1).
This news story corresponds to the story on the lower left hand corner of the News webpage W2.
The hyperlink in 3D is equivalent, from a content perspective, to the simple movement of a mouse or shift of a glance from point 1 in W2 to point 2. If the user corresponding to avatar 4 (A4) decides she wants to continue reading the story in 2D she can, with a simple right click. The most critical piece here is that the 2D view that emerges will be focused on the story in the news cube in W(3,2). The focus could be partial, with other parts of the website visible. Or the story could be in a separate tab.
The movement of A4 from t to t1 is represented succinctly by the equations:
W(3,1) → W(3,2) = W(2,1) → W(2,2) = A4t → A4t1
Page 2: Introducing the Visual Cone
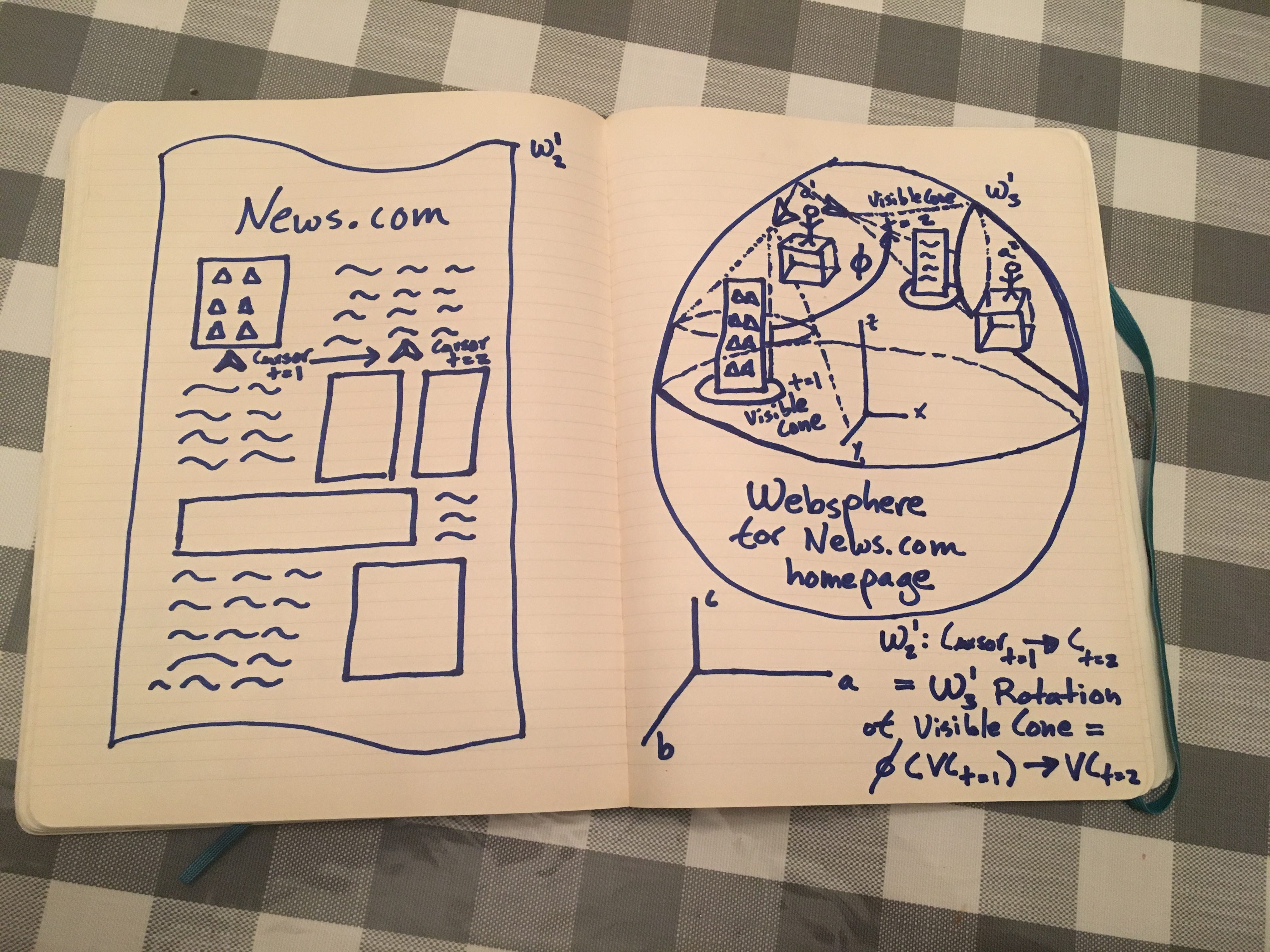
In this image we introduce the concept of the visible cone, which will be critical throughout this article. An avatar in a 3D worldsphere can only see a certain portion of that sphere at any given time. This is no different from our experience in real life (IRL) where we cant see what is behind us. For simplification purposes, we do not consider peripheral vision here, nor do we go into the various spans of view provided by virtual reality devices. Here we assume a 90 degree field of view for simplicity, even though headsets such as the Oculus Rift and HTC Vive are in the 100–110 degree range and, others such as Star VR claim to reach 180 degrees. The way we represent the visible cone is by defining three spherical coordinates, setting the avatar’s eyes as the origin, and drawing three lines at a 45 degree angle along each coordinate. We extend the lines until they reach the boundary of the sphere. The three points of intersection define a plane. The intersection of that plane with the sphere is an ellipse. If we imagine “filling in” the space between the ellipse and the three lines, moving backwards from the periphery of the sphere to the avatar, we can see that it is represented by a cone. This cone is a formalism that approximates the field of view of the avatar, given the avatar’s position in (a,b,c) universal coordinates, (x,y,z) local coordinates, and the direction of her gaze, which we will later define with three separate spherical coordinates.
In this example, we define the 3D equivalent of moving a mouse cursor from a picture, on the upper left hand corner of a news website, to its corresponding text, on the upper right hand corner of the 2D website. In the 3D web, one of the representations of this movement, is a rotation PHI along one of the spherical axis that define the visible cone of the avatar. Essentially, the avatar is moving his head such that the focus of his gaze moves from a news cube with the picture to a news cube with the text. Note that the text cube is “floating” in the websphere. This is done explicitly to show that 3D objects are not limited to the central circular bisection of the sphere.
Notice that there is another avatar (a2) in the scene. She is initially not in the visible cone of a1, which we write as VC(a1,t1). After the rotation PHI of a1’s gaze, a1 is now inside the new visible cone VC(a1,t2). We will talk more about the relationship between various avatars in a websphere in later sections.
Page 3: Defining the Avatar function
Here we crystalize the 10 dimensional representation of the avatar a1 in a websphere W(3,1) at time t1. An avatar a1 has a total of 9 spacial dimensions — 3 local dimensions (x,y,z), 3 universal dimensions (a,b,c) and 3 spherical dimensions representing the visible cone (alpba, beta, lambda). Adding the time dimension t we see that any function or operator applied to an avatar must take into account 10 dimensions. We can think of a1 as a vector with 10 entries, or a 1X10 matrix. Matrix multiplication is a helpful tool for studying transformations in the real physical world, so it is no surprise that it would be helpful in understanding the 3D or “virtual” web.
We should make a quick note here, that webpsheres can be, arbitrarily, fixed in (a,b,c) universal space. That means that they do not move relative to the universal coordinate system. If we decided to place such a restriction on a set of webspheres, we would avoid issues such as rotation and acceleration, which would complicate our formalism tremendously. In practice, the only concept we will need is the rotation of a websphere around its origin, which we will discuss later. One way of interpreting the “fixing” of a websphere in (a,b,c) space is that the IP address that represents it — a yet to be defined 3D IP representing a virtual environment — cannot change. Perhaps this means that the same cluster of server or the same data center will house the GPUs that render the websphere. In any case, in such a situation only 7 dimensions are relevant for defining the avatar function A because the absolute values of (x-a), (y-b), and (z-c) are constant for any point (x,y,z) on the sphere.
Let us now define certain sets of 3D objects inside worlspheres. We can say that the set E(a(1,1)) is the set of avatars a2, a3 and a4 that are in the visible cone of a1 at time t1. If we apply a rotation PHI(1,2) — which means a rotation with magnitude PHI that occurs between t1 and t2 — to the gaze of a1, then he will no longer be able to see a2, a3, and a4, but will now have a clear view of a5. At t2 the set E(a(1,2)) has only one member, which is a5. Of course the reality is that all three visual cone dimensions (spherical dimensions) alpha, beta, and lambda have been rotated and PHI represents the composite rotation. In other words, the rotation PHI(1,2) is made up of three components: alpha(1,2), beta(1,2), and lambda(1,2). But for the sake of simplification we will only consider PHI here. Note that this concept of object sets is not limited to avatars but can be extended to any object in the visible cone of a1. We could, of course, define the set of objects in the whole worlsphere W(3,1) which we would denote E(W(3,1)).
Page 4: Dynamically updated 2D Analogs for interactions in 3D Social Networks
Let’s extend concepts we have discussed into more practical settings, such as a social network in the 3D web. In some research, this is referred to as a CVE or collaborative virtual environment. Id like to start by clarifying that I don’t intend to explore the relationship between avatars in 3D worlds here. Rather, I am focused on defining the link between the interaction of those avatars in 3D and their representations in the existing 2D web.
Let’s define the concept of a visual social network of avatar a1 at time t1 denoted as VS (a(1,1))
This is a set that has two subsets. The first is the set E(a(1,1)) of all avatars visible from a1 at time t1.
The second subset is the set T(1) of timeline data corresponding to the avatars in E(a(1,1)). Timeline data can include text, video, audio, photos, 3D content, VR/AR content, and any other media that is yet to be invented. We can thus say that VS(a(1,1)) = {E(a(1,1)), T(1)}. T(1,a2) represents a subset of T(1) which includes only postings from avatar a2 before time t1. Note that the 2D representation of VS(a(1,1)) is the well known existing timeline view of current social networks on the 2D web.
Applying a rotation in the visible cone PHI(1,2) that spans the time t1 to t2 yields a new visible social network VS(a(1,2)) = {E(a(1,2), T(2)}. Going back to the example in Page 3, we can see that VS(a(1,2)) = {a5, T(2,a5)}. This can be read as follows “The visual social network of avatar 1 at time 2 includes the following subsets — the set of visible avatars at time 2, which is only a5, and the set of postings made by avatar 5 before time 2.
Now lets think about the evolution of a visible social network over time. Note that we can generalize this line of thinking to any set of objects or relationships between objects in a 3D websphere. Lets define an operator Z (pronounced Zeta) which acts on the avatar function A — remember this is the 10 dimensional function we previously explored. More specifically, consider an operator Z(PHI), pronounced Zeta Phi, which has the effect of rotating the visible cone of a1 from time t1 to time t2. We can define a cross product Z(PHI) X a(1,1) which neatly represents this effect. Note that a rotation of the visible cone of a1 could change the visible social network of a1. The new visible social network is defined as VS(a(1,2))
Since other avatars (such as a2, a3, a4, a5 in picture 3) can move from t1 to t2 (the time it takes to rotate the visible cone of a1 by PHI) then VS(a(1,2)) depends on the avatar function for a1 AND the individual avatar functions for all other avatars in the websphere W(3,1).
Page 5–8: The Communicable Social Network
Now let’s define a subset of the visible social network called the “Communicable Social Network”. Note that this term, denoted CS(W(3,1), 1) is not tied to a particular avatar. It is tied to the websphere. This term is read as “the communicable social network at t1 of the websphere W(3,1)” and is defined as the set consisting only of avatars who’s visible cone intersects the visible cone of at least one other avatar in W(3,1) at t1.
Thus, if a1 is looking directly at a2 and vice versa, but all other avatars (a3…a5) are looking in away from a1 and a2, then the communicable social network will be CS(W(3,1),1) = {(a1,a2)}. If all the avatars are standing in a circle and they are all visible to each other then CS(W(3,1),1) = {(a1,a2….a5)}
Note that an avatar a2 can be in the visible social network VS(a1,1) but NOT in the communicable social network CS(W(3,1),1). This would occur if a1 is looking at a2, but a2 is looking in the opposite direction of a1. That is, just because my avatar can see you, does not mean that my avatar can communicate with you. Of course this is based on the assumption that communication must be transmitted in a visual form. In virtual worlds like second life, the concept of “near chat” is defined where avatars within a certain radius of each other on a virtual grid are able to have group conversations with each other via chat or voice. The essence of CS is not tied to the form of communication. Its purpose is to define a group that can interact at a particular time on a worldsphere. We can imagine that the 2D representation of 3D social networks could use both the concept of VS and CS. For example, you might want to see, in 2D the posts of all avatars that are visible to you in your worldsphere. Alternatively, you might only be interested in the posts of avatars that can ALSO see you. It is similar to the concept of “available” in chat applications. Your full list of contacts in the chat application would be analogous to the VS, while CS would represent only your contacts that are available to chat.
Pages 7 -10: 2D Analogs for Visual and Communicable Social Networks in 3D
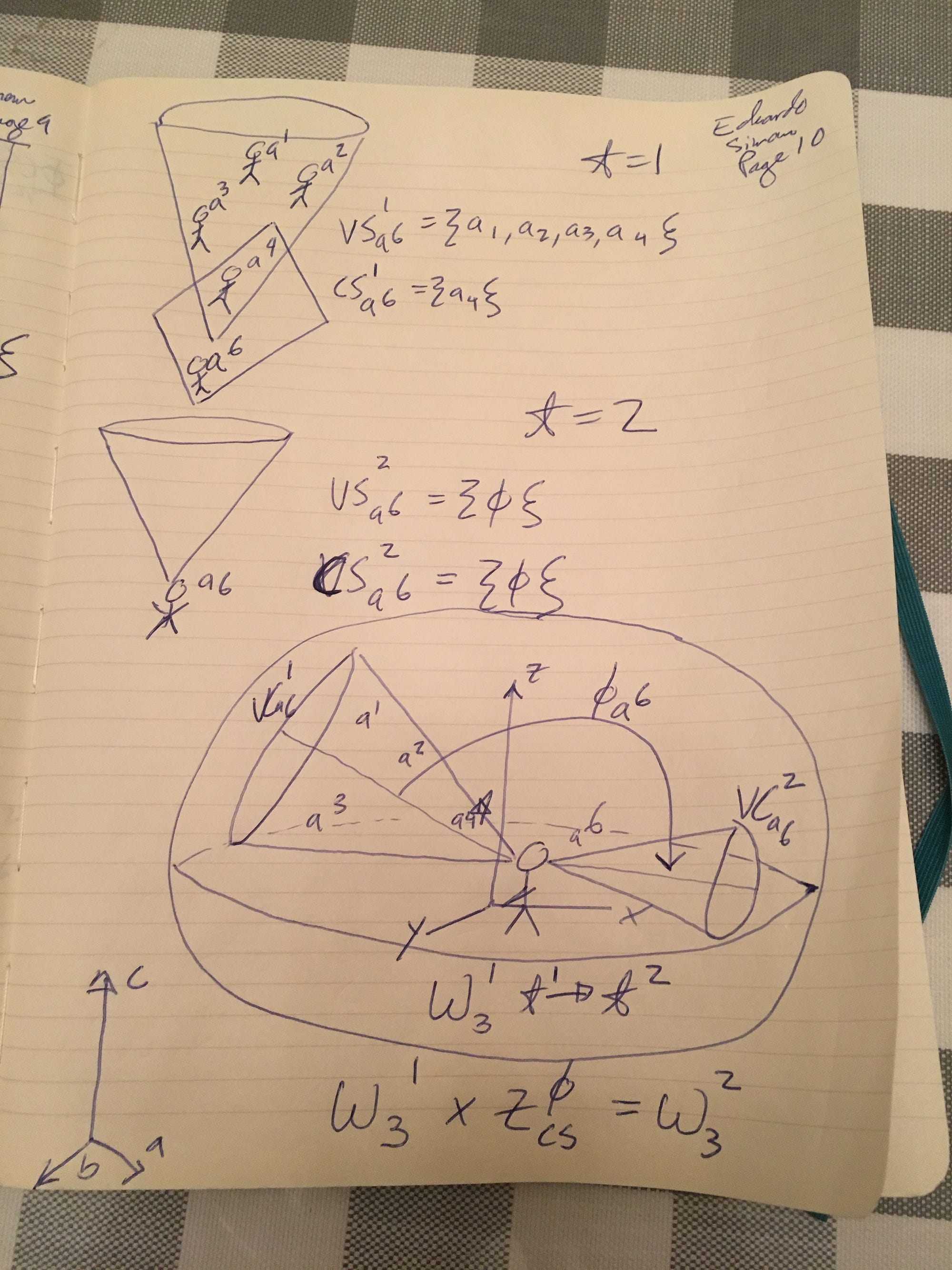
Let’s consider a worldsphere with six avatars (a1…..a6) at time t1. As you can see in the first diagram on page 7, the avatars are looking all over the place. The visual cones of each avatar are represented in the drawing. The only two avatars who can see each other in this scenario are a1 and a2. Notice that many of the visual cones intersect or overlap — but that does not mean that the avatars the cones corresponding can see each other. Thus in this case CS(W(3,1),1) is {a1, a2}
Now imagine we apply the operator Z(PHI) which has the effect of rotating all of the avatars’ gazes by a particular angle. That angle can be different for each avatar. After this transformation, the new CS(W(3,1,),2) is {a1,a3}. In addition the visible social networks of each of the avatars has also changed, as shown in page 9.
For example, lets take avatar a6. At t1, her VS(a6,1) = {a1,a2,a3,a4*}. Note that a4 is the only member of her VS that is also a member of the CS for the websphere. We denote that with a *
After the operator Z(PHI) is applied, the new VS for a6 is VS(a6,2) = { Null }. That is, the visible social network for a6 has completely disappeared. And of course a6 is no longer part of the CS of W(3,1).
We can think of the boxes drawn on page 9 as a possible 2D representation of the VS and CS of a particular avatar. You can imagine that if you are the human corresponding to a6, when you log in to your social media account in 2D, you will immediately see that there are four avatars in your VS and 1 in your CS. If you were only operating in a 2D web environment, this might be too restrictive. After all, you would want to see information from all your friends regardless of where they are physically or virtually.
But the point of this article is to define useful 2D analogs for 3D environments. And if your end goal is to interact, at least partially in 3D, then you want to ONLY see avatars that are visible to your avatar, and you want to know right away what avatars can communicate with you visually. Of course the idea of a discrete operator Z(PHI) from time t1 to t2 is a great simplification here. The avatars in this worldsphere will be free to move at any time along any of the 9 spacial dimensions. Thus, if you are looking at your 2D social media feed, you would see a constantly updating list of VS and CS. One possible use case would be for a group meetup in 3D (of course this could be VR or AR as well). You might want to wait until you see that all of your friends’ avatars are in both your VS and CS before putting on your headset.
Its also conceivable that when you are in VR/AR wearing a headset, the 2D analogue could be helpful as a guide — perhaps displayed as a pane of glass next to your left controller. It would be much easier to figure out what avatars are in your VS and CS from a quick glance to the 2D pane than having to walk around the whole websphere looking for other avatars — especially since they are moving!
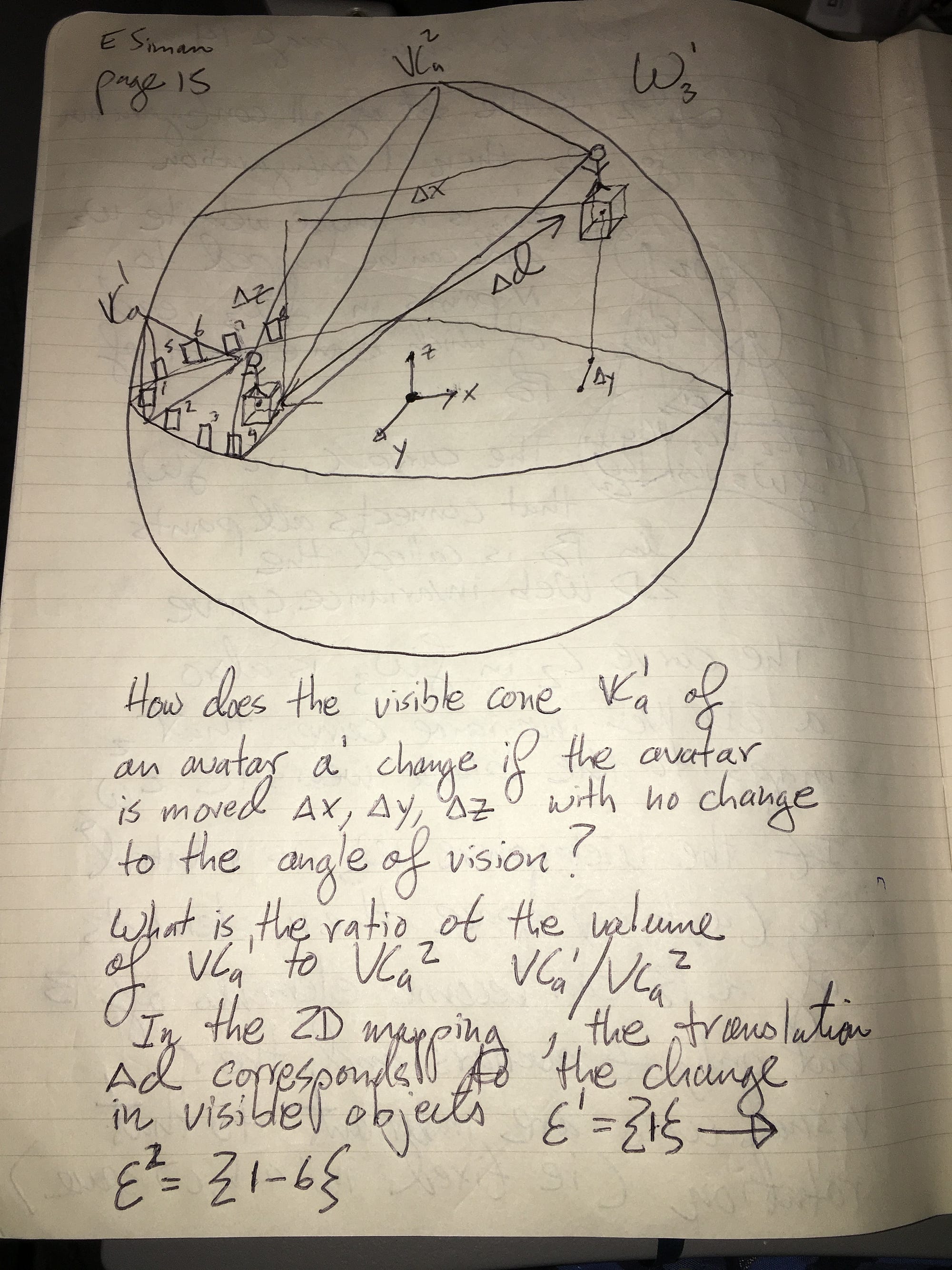
Pages 11–25: Ideas for tracking 3D/VR/AR E-Commerce activities in existing 2D formats. + Manifolds!
Page 25: A brief explanation
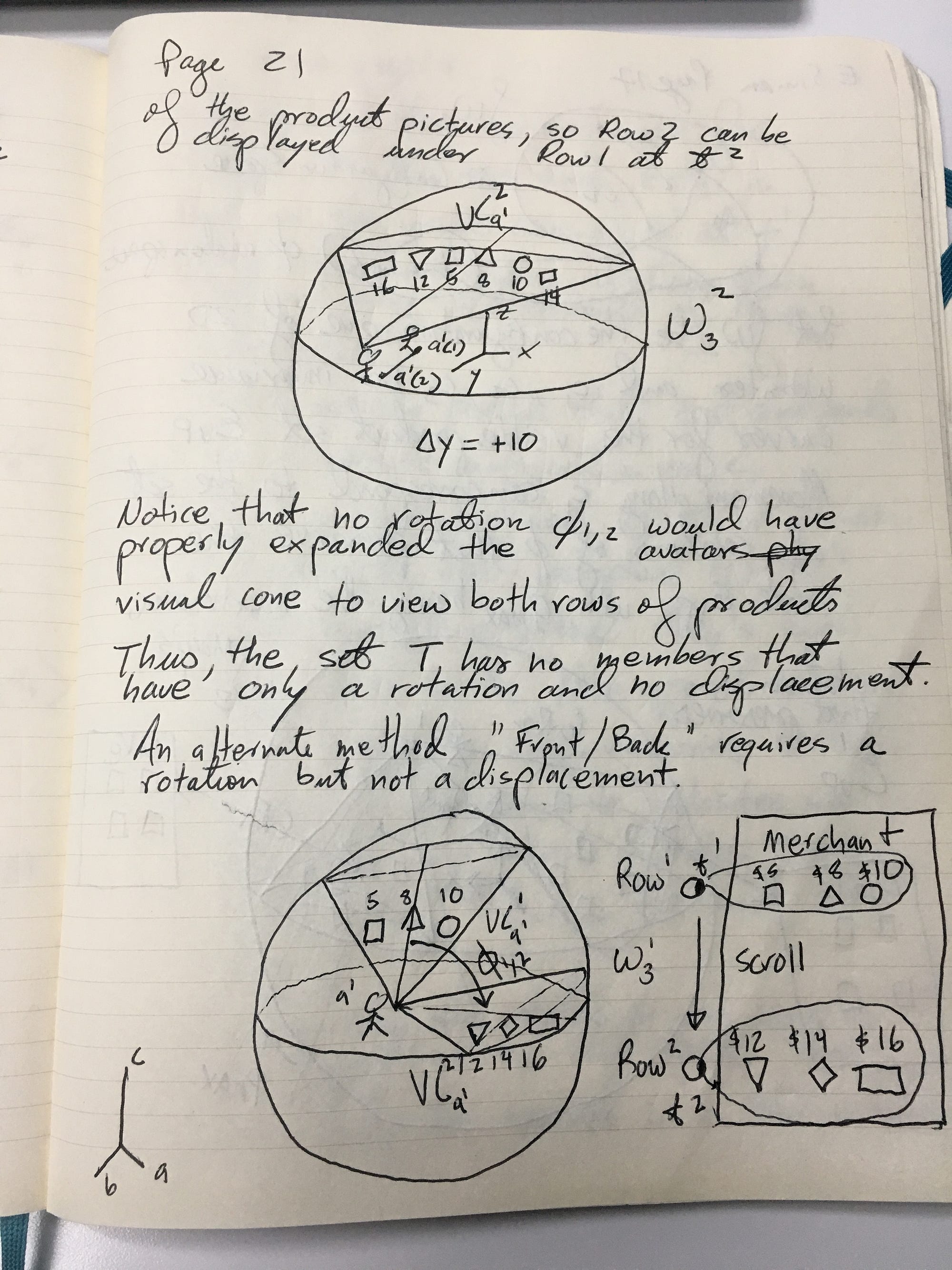
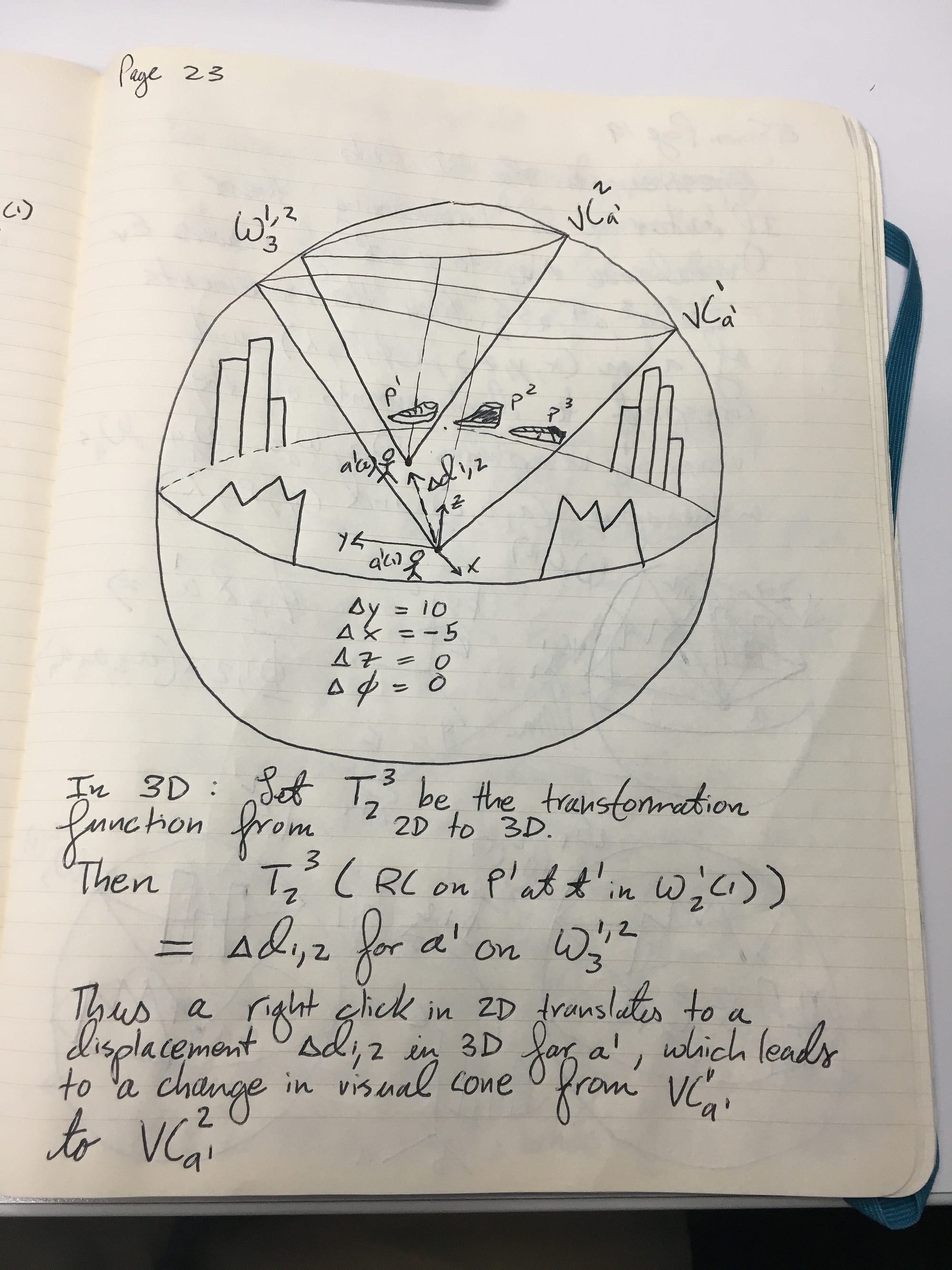
The subset Dxy of D has the representation in 3D on W3,1(1,2) of a semi-circle on a circular cross section through the center of the sphere.
This set Dxy of 3D displacements corresponds to T(3,2), a transformation from 3D to 2D representing a Right Click on product P1 at t1